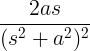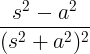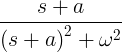拉普拉斯变换
拉普拉斯变换通过从零到无穷的积分将时间域函数转换为s域函数，乘以 e-st。
拉普拉斯变换用于快速求解微分方程和积分。
时间域中的导数变换为s域中的乘法。
时间域中的积分变换为s域中的除法。
拉普拉斯变换函数
拉普拉斯变换用 L{} 运算符定义：
拉普拉斯逆变换
可以直接计算拉普拉斯逆变换。
通常逆变换从变换表中给出。
拉普拉斯变换表
| 函数名 | 时间域函数 | 拉普拉斯变换 |
|---|---|---|
|
f (t) |
F(s) = L{f (t)} |
|
| 常数 | 1 |  |
| 线性 | t |  |
| 幂 |
t n |
|
| 幂 |
t a |
Γ(a+1) ⋅ s -(a+1) |
| 指数 |
e at |
|
| 正弦 |
sin at |
|
| 余弦 |
cos at |
|
| 双曲正弦 |
sinh at |
|
| 双曲余弦 |
cosh at |
|
| 增长正弦 |
t sin at |
|
| 增长余弦 |
t cos at |
|
| 衰减正弦 |
e -at sin ωt |
|
| 衰减余弦 |
e -at cos ωt |
|
| δ函数 |
δ(t) |
1 |
| 延迟δ函数 |
δ(t-a) |
e-as |
拉普拉斯变换性质
| 属性名 | 时域函数 | 拉普拉斯变换 | 注释 |
|---|---|---|---|
|
f (t) |
F(s) |
||
| 线性性 | a f (t)+bg(t) | aF(s) + bG(s) | a,b 是常数 |
| 尺度变换 | f (at) |
|
a>0 |
| 平移 | e-at f (t) | F(s + a) | |
| 延迟 | f (t-a) | e-asF(s) | |
| 导数 |
|
sF(s) - f (0) | |
| N阶导数 |
|
snf (s) - sn-1f (0) - sn-2f '(0)-...-f (n-1)(0) | |
| 幂函数 | t n f (t) |
|
|
| 积分 |
|
|
|
| 倒数 |
|
|
|
| 卷积 | f (t) * g (t) | F(s) ⋅ G(s) | * |
| 周期函数 | f (t) = f (t+T) |
|
拉普拉斯变换示例
示例 #1
找到 f(t) 的变换：
f (t) = 3t + 2t2
解：
ℒ{t} = 1/s2
ℒ{t2} = 2/s3
F(s) = ℒ{f (t)} = ℒ{3t + 2t2} = 3ℒ{t} + 2ℒ{t2} = 3/s2 + 4/s3
示例 #2
找到 F(s) 的逆变换：
F(s) = 3 / (s2 + s - 6)
解：
为了找到逆变换，我们需要将 s 域函数改为一个更简单的形式：
F(s) = 3 / (s2 + s - 6) = 3 / [(s-2)(s+3)] = a / (s-2) + b / (s+3)
[a(s+3) + b(s-2)] / [(s-2)(s+3)] = 3 / [(s-2)(s+3)]
a(s+3) + b(s-2) = 3
为了找到 a 和 b，我们得到 2 个方程 - 第一个是 s 系数，第二个是其余部分：
(a+b)s + 3a-2b = 3
a+b = 0 , 3a-2b = 3
a = 3/5 , b = -3/5
F(s) = 3 / 5(s-2) - 3 / 5(s+3)
现在 F(s) 可以通过使用指数函数的变换表轻松变换：
f (t) = (3/5)e2t - (3/5)e-3t