二次方程

二次方程是一个有三个系数 - a, b, c - 的二次多项式。

二次方程的表达式为：

ax²+ bx + c = 0

二次方程的解由两个数 x₁ 和 x₂ 给出。

我们可以将二次方程变形成以下形式：

(x - x₁)(x - x₂) = 0

二次公式

二次方程的解由二次公式给出：

平方根内的表达式称为判别式，用 Δ 表示：

Δ = b² - 4ac

带有判别式符号的二次公式：

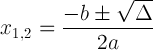
这个表达式很重要，因为它能告诉我们解的情况：

当 Δ>0，有两个实数根 x₁=(-b+√Δ)/(2a) 和 x₂=(-b-√Δ)/(2a)。
当 Δ=0，有一个根 x₁=x₂=-b/(2a)。
当 Δ<0，没有实数根，有两个复数根：
x₁=(-b+i√-Δ)/(2a) 和 x₂=(-b-i√-Δ)/(2a)。

问题 #1

3x²+5x+2 = 0

解答：

a = 3, b = 5, c = 2

x_1,2 = (-5 ± √(5² - 4×3×2)) / (2×3) = (-5 ± √(25-24)) / 6 = (-5 ± 1) / 6

x₁= (-5 + 1)/6 = -4/6 = -2/3

x₂= (-5 - 1)/6 = -6/6 = -1

问题 #2

3x²-6x+3 = 0

解答：

a = 3, b = -6, c = 3

x_1,2 = (6 ± √( (-6)² - 4×3×3)) / (2×3) = (6 ± √(36-36)) / 6 = (6 ± 0) / 6

x₁= x₂= 1

问题 #3

x²+2x+5 = 0

解答：

a = 1, b = 2, c = 5

x_1,2 = (-2 ± √(2² - 4×1×5)) / (2×1) = (-2 ± √(4-20)) / 2 = (-2 ± √(-16)) / 2

没有实数解。这些值是复数：

x₁= -1 + 2i

x₂= -1 - 2i

二次函数图

二次函数是一个二次多项式函数：

f(x) = ax² + bx + c

二次方程的解是二次函数的根，也是二次函数图像与 x 轴的交点，当

f(x) = 0

当图像与 x 轴有两个交点时，二次方程有两个解。

当图像与 x 轴有一个交点时，二次方程有一个解。

当图像与 x 轴没有交点时，我们没有实数解（或者有两个复数解）。