积分
积分是导数的逆运算。
函数的积分是函数图形下方的面积。
不定积分定义
当
![]()
不定积分属性
![]()
![]()
![]()
![]()
![]()
![]()
积分变量的变化
当
![]() 和
和
![]()
![]()
分部积分
![]()
积分表
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
定积分定义
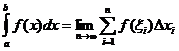
当
![]()
![]()
![]()
定积分计算
当
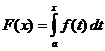 ,
,
![]()
![]() 和
和
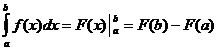
定积分性质
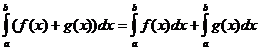
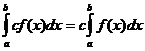
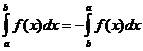
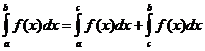
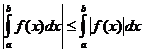
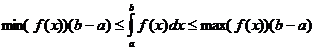 当
当
![]()
积分变量的变化
当
![]() ,
,
![]() ,
,
![]() ,
,
![]()
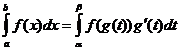
按部分集成
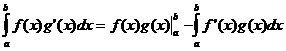
中值定理
当
f(x)
是连续的,有一个点
![]() so
so
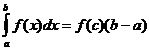
定积分的梯形逼近
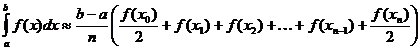
Gamma函数
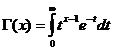
Gamma函数收敛于 x>0.
Gamma函数属性
G(x+1) = xG(x)
G(n+1)
= n!
,
当
n
![]() ℕ
(正整数).
ℕ
(正整数).
Beta函数
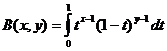
贝塔函数与伽玛函数的关系