零数 (0)
零数定义
零是数学中用来描述没有数量或空数量的数。
当桌子上有2个苹果,我们拿走这2个苹果后,我们可以说桌子上没有苹果了。
零数既不是正数也不是负数。
零也是其他数中的占位数字(例如:40,103,170)。
零是数字吗?
零是一个数字。它既不是正数也不是负数。
零数位
零数位在写数字时用作占位符。
例如:
204 = 2×100+0×10+4×1
零数历史
谁发明了零数?
现代零(0)符号是在6世纪由印度人发明的,后来被波斯人和阿拉伯人使用,然后传入欧洲。
零的符号
零数用0符号表示。
阿拉伯数字系统使用符号٠。
零数特性
x代表任何数。
| 操作 | 规则 | 例子 |
|---|---|---|
加法 |
x + 0 = x |
3 + 0 = 3 |
减法 |
x - 0 = x |
3 - 0 = 3 |
乘法 |
x × 0 = 0 |
5 × 0 = 0 |
除法 |
0 ÷ x = 0 ,当 x ≠ 0 |
0 ÷ 5 = 0 |
|
x ÷ 0 未定义 |
5 ÷ 0 未定义 |
|
指数 |
0 x = 0 |
05 = 0 |
|
x 0 = 1 |
50 = 1 |
|
根号 |
√0 = 0 |
|
对数 |
logb(0) 未定义 |
|
|
|
||
阶乘 |
0! = 1 |
|
正弦 |
sin 0° = 0 |
|
余弦 |
cos 0° = 1 |
|
正切 |
tan 0° = 0 |
|
导数 |
0' = 0 |
|
积分 |
∫ 0 dx = 0 + C |
|
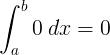
|
零的加法
一个数字加零等于该数字:
x + 0 = x
例如:
5 + 0 = 5
零的减法
一个数字减零等于该数字:
x - 0 = x
例如:
5 - 0 = 5
乘以零
一个数字乘以零等于零:
x × 0 = 0
例如:
5 × 0 = 0
被零除
一个数字除以零没有定义:
x ÷ 0 is undefined
例如:
5 ÷ 0 is undefined
零除以一个数字
零除以一个数字等于零:
0 ÷ x = 0
例如:
0 ÷ 5 = 0
零的零次幂
一个数的零次幂等于一:
x0 = 1
例如:
50 = 1
零的对数
以底数 b 的对数零是没有定义的:
logb(0) is undefined
没有一个数能够使底数 b 的幂等于零。
只有当 x 趋向于零时,底数 b 的对数的极限是负无穷:
![]()
包含零的集合
零是自然数、整数、实数和复数集合的元素:
| 集合 | 集合成员表示法 |
|---|---|
| 自然数(非负整数) | 0 ∈ ℕ0 |
| 整数 | 0 ∈ ℤ |
| 实数 | 0 ∈ ℝ |
| 复数 | 0 ∈ ℂ |
| 有理数 | 0 ∈ ℚ |
零是偶数还是奇数?
偶数的集合是:
{... ,-10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
奇数的集合是:
{... ,-9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
零是 2 的整数倍:
0 × 2 = 0
零是偶数的一个成员:
0 ∈ {2k, k∈ℤ}
所以零是一个偶数,不是奇数。
零是自然数吗?
自然数集有两种定义。
非负整数集:
ℕ0 = {0,1,2,3,4,5,6,7,8,...}
正整数集:
ℕ1 = {1,2,3,4,5,6,7,8,...}
零是非负整数集的一个成员:
0 ∈ ℕ0
零不是正整数集的一个成员:
0 ∉ ℕ1
零是整数吗?
整数的定义有三种:
整数集:
ℤ = {0,1,2,3,4,5,6,7,8,...}
非负整数集:
ℕ0 = {0,1,2,3,4,5,6,7,8,...}
正整数集:
ℕ1 = {1,2,3,4,5,6,7,8,...}
零是整数集和非负整数集的一个成员:
0 ∈ ℤ
0 ∈ ℕ0
零不是正整数集的一个成员:
0 ∉ ℕ1
零是整数吗?
整数集:
ℤ = {0,1,2,3,4,5,6,7,8,...}
零是整数集的一个成员:
0 ∈ ℤ
所以零是一个整数。
零是有理数吗?
有理数是可以表示为两个整数的商的数:
ℚ = {n/m; n,m∈ℤ}
零可以写成两个整数的商。
例如:
0 = 0/3
所以零是一个有理数。
零是正数吗?
正数被定义为大于零的数:
x > 0
例如:
5 > 0
因为零不大于零,所以它不是一个正数。
零是素数吗?
数字零不是素数。
零不是正数,并且有无穷多个约数。
最小的素数是2。