基础概率公式

 

概率范围

0 ≤ 概率(A) ≤ 1

互补事件规则

P(A^C) + P(A) = 1

加法规则

P(A∪B) = P(A) + P(B) - P(A∩B)

互斥事件

事件A和B互斥当且仅当

概率(A∩B) = 0

条件概率

概率(A | B) = P(A∩B) / P(B)

贝叶斯公式

概率(A | B) = P(B | A) ⋅ P(A) / P(B)

独立事件

事件A和B独立当且仅当

概率(A∩B) = 概率(A) ⋅ 概率(B)

累积分布函数

F_X(x) = P(X ≤ x)

概率质量函数

概率密度函数

 

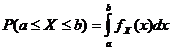
协方差

相关系数

 

伯努利: 0-失败 1-成功

几何分布: 0-失败 1-成功

超几何分布: N个物体中有K个成功的物体，取n个物体。