概率分布
在概率论和统计学中,分布是随机变量的特征,描述了每个值的随机变量的概率。
每个分布都有一个确定的概率密度函数和概率分布函数。
虽然概率分布有无限多种,但常用的几种分布是:
累积分布函数
概率分布由累积分布函数 F(x) 描述,
这是随机变量 X 取得小于或等于 x 的值的概率:
F(x) = P(X ≤ x)
连续分布
累积分布函数 F(x) 是连续随机变量 X 的概率密度函数 f(u) 的积分计算而得。
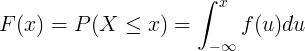
离散分布
累积分布函数 F(x) 是离散随机变量 X 的概率质量函数 P(u) 的求和计算而得。
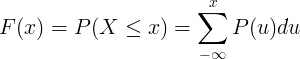
连续分布表
连续分布是连续随机变量的分布。
连续分布示例
...
连续分布表
| 分布名称 | 分布符号 | 概率密度函数(pdf) | 均值 | 方差 |
|---|---|---|---|---|
|
fX(x) |
μ = E(X) |
σ2 = Var(X) |
||
| 正态分布 |
X ~ N(μ,σ2) |
|
μ | σ 2 |
| 均匀分布 |
X ~ U(a,b) |
|
|
|
| 指数分布 | X ~ exp(λ) |
|
|
|
| 伽马分布 | X ~ gamma(c, λ) |
x > 0, c > 0, λ > 0 |
|
|
| 卡方分布 |
X ~ χ 2(k) |
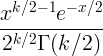
|
k |
2k |
| Wishart分布 | ||||
| F分布 |
X ~ F (k1, k2) |
|||
| 贝塔分布 | ||||
| 威布尔分布 | ||||
| 对数正态分布 |
X ~ LN(μ,σ2) |
|||
| 瑞利分布 | ||||
| 柯西分布 | ||||
| 狄利克雷分布 | ||||
| 拉普拉斯分布 | ||||
| 莱维分布 | ||||
| 赖斯分布 | ||||
| 学生t分布 |
离散分布表
离散分布是离散随机变量的分布。
离散分布示例
...
离散分布表
| 分布名称 | 分布符号 | 概率质量函数 (pmf) | 均值 | 方差 | |
|---|---|---|---|---|---|
|
fx(k)
= P(X=k)
k = 0,1,2,... |
E(x) | Var(x) | |||
| 二项分布 |
X ~ Bin(n,p) |
|
np |
np(1-p) |
|
| 泊松分布 |
X ~ Poisson(λ) |
|
λ ≥ 0 |
λ |
λ |
| 均匀分布 |
X ~ U(a,b) |
|
|
|
|
| 几何分布 |
X ~ Geom(p) |
|
|
|
|
| 超几何分布 |
X ~ HG(N,K,n) |
|
N = 0,1,2,... K = 0,1,..,N n = 0,1,...,N |
|
|
| 伯努利分布 |
X ~ Bern(p) |
|
p |
p(1-p) |
|