方差

在概率与统计中，随机变量的方差是指从平均值的平方距离的平均值。它表示随机变量在接近平均值的分布情况。小方差表示随机变量接近平均值分布。大方差表示随机变量远离平均值分布。例如，正态分布中，窄钟形曲线会有小方差，宽钟形曲线会有大方差。

随机变量X的方差是X与期望值μ之差的平方的期望值。

σ² = Var ( X ) = E [(X- μ)²]

根据方差的定义我们可以得到

σ² = Var ( X ) = E(X²) - μ²

对于均值为μ和概率密度函数f(x)的连续随机变量：

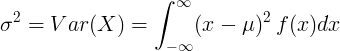
$\sigma ^2=Var(X)=\int_{-\infty }^{\infty }(x-\mu)^2\: f(x)dx$

或

$Var(X)=\left [ \int_{-\infty }^{\infty }x^2\: f(x)dx \right ]-\mu^2$

对于均值为μ和概率质量函数P(x)的离散随机变量X：

$\sigma ^2=Var(X)=\sum_{i}^{}(x_i-\mu _X)^2P_X(x_i)$

或

$Var(X)=\left [ \sum_{i}^{}x_i^2P(x_i) \right ]-\mu^2$

当X和Y是独立随机变量时：

另见