反正弦函数
arcsin(x), sin-1(x), 反正弦函数。
反正弦定义
当 -1 ≤ x ≤ 1 时,x 的反正弦被定义为 x 的反正弦函数。
当 y 的正弦等于 x 时:
sin y = x
则 x 的反正弦等于 x 的反正弦函数,也等于 y:
arcsin x = sin-1 x = y
例子
arcsin 1 = sin-1 1 = π/2 弧度 = 90°
反正弦图像
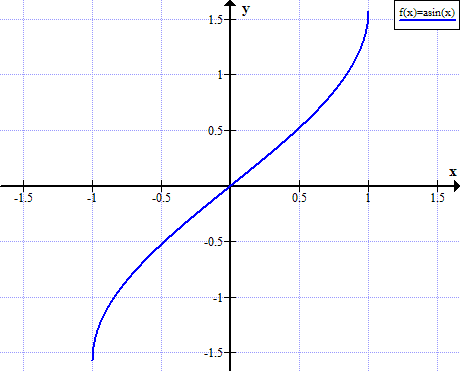
反正弦规则
| 规则名称 | 规则 |
|---|---|
| 反正弦的正弦 | sin( arcsin x ) = x |
| 正弦的反正弦 | arcsin( sin x ) = x+2kπ, 当 k∈ℤ (k 为整数) |
| 负参数的反正弦 | arcsin(-x) = - arcsin x |
| 互补角 | arcsin x = π/2 - arccos x = 90° - arccos x |
| 反正弦和 | arcsin α + arcsin(β) = arcsin( α√(1-β2) + β√(1-α2) ) |
| 反正弦差 | arcsin α - arcsin(β) = arcsin( α√(1-β2) - β√(1-α2) ) |
| 反正弦的余弦 | |
| 反正弦的正切 | |
| 反正弦的导数 | 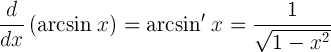 |
| 反正弦的不定积分 |
反正弦表
| x | arcsin(x) (弧度) |
arcsin(x) (°) |
|---|---|---|
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |